Thesis Outline

http://mit.edu/hon/Public/blah.html

Committee Meeting 3 Slides

http://mit.edu/hon/Public/blah.html

VRP Results with Optimal Path Completion

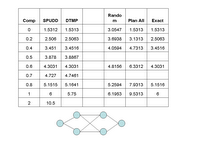
Here are results for the 4 vehicle, 8 targets case with low fuel, where the targets are grouped by twos into quadrants. DTMP uses a decision tree to categorize problem instances.

the difference is :
From the training data, the sub-problems associated with the optimal solution are saved at the corresponding leaves. When a problem instance is categorized at a leaf, all of the optimal sub-problems from previous training samples are tested and the ones resulting in the best value for that particular problem instance are added to the set of interesting sub-problems for the master level IP. Computation costs associated with this operation, only includes that of solving for sub-problems that are included in the set set of interesting sub-problems, and does not include all sub-problems that were tested.

Learning Subproblems Additions for the m-TSP

Base Level Problem: Given a set of colocated homogeneous vehicles, a set of targets and their locations and their values, and a fuel constraint on vehicles, execute a set of tours that maximize the total value minus the tour length while satisfying the fuel constraint.

Problem Approach: The problem is hierarchically decomposed into a master level problem and subproblems. The subproblems consist of missions for the vehicles (i.e. the vehicles are assigned a subset of targets and must generate a tour where each target in the subset is visited once without violating the fuel constraint). The subproblems are characterized by a mission value, which is comprised of the value of the targets visited during the mission minus the cost of the tour, and the subset of targets visited. The master level problem is formulated as an binary integer program which selects from the set of subproblem, those with maximize the total value while satisfying the constraint that no target is ever visited more than once.

Meta-level Problem: The meta-level problem is to determine a policy for generating interesting subproblems given the results of the current set of subproblems. Solving subproblems take time. As a first pass the goal of the meta-level planner will be to maximize the following objective function:

sum(Value of Missions Selected) - epsilon*(WallClockTimeForGeneratingSubproblems)


In the future, we plan to apply add windows of opportunity to the problem, such that the targets will have start and end times which specify when they are available to be service by the vehicles. In this situation, a more natural objective function for the meta-level planner will be to just maximize the sum of the mission value. The epsilon weighting factor for the time cost will no longer be explicitly necessary, as the total time taken for solving subproblems will interact with the windows of opportunities of the targets to generate implicit time costs.



The graph to the right is a preliminary result for the case of 2 vehicles and 4 targets located in a 2x2 region with fuel constraint of 4. The target were each valued at 10 each. note the legend is mislabelled. I have plotted on the graph the results of the DTMP, Plan all and a Greedy Strategy for varying values of epsilon. The Plan All policy assumes that all 2^4 or 16 subproblems were generated prior to solving the master level problem. The Greedy Algorithm consisted of alternating vehicles selecting the nearest target to add to its subset. The DTMP result does not perform as well as the plan all strategy for epsilon= 0. I believe that the decision tree which dictates the order of subproblem generation stop short in many cases resulting the what I referred to as the path completion problems in previous posts.


The case for 4 vehicles and 8 targets over a 2x2 region with fuel = 4 is posted below. The poor performance may be due to insufficient sampling in addition to the path completion problem.



I am currently working to correct this problem.

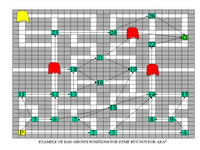
Example of Path Completion Problem

The path completion problem involves cases where the decision tree does not provide enough looks to find a complete path to the goal. Under these circumstances, I find the *optimal* path using the true arc costs of the known arcs, and the worst-case cost of the unknown arcs.


Example
In this example, I show that the path completion problem is present even in the zero-computation cost case. For a particular arc cost instantiation =
[1 1 0 1 1 1 1 0 1 1 0 0 1 0 0 0 ], where 0 means an arc cost of 0 and 1 means a cost of 2, we see that the decision tree recommends looking at arcs 2,1,8,3. The mean predicted cost of th optimal path given the known arc costs is supposed to be 2 with std = 0. The optimal path completion arcs should be 14 and 16.

However, when executing the policy, the path completion algorithm selected arcs 13 and 15 to complete the path. Since neither arcs 13,14,15, nor 16 were known, they were assumed to take their worst-case values. This made the cost of executing 13-15 equivalent to 14-16, when in actuality the latter has lower cost.


Fix
In order to distinguish between good and bad completion paths, I tried assuming expected arc costs for the unknown arcs rather than their worst case costs. This improved the solution cost drastically.

I originally used worst-case costs as estimates of arc costs because I was doing state aggregation using quality levels. The quality estimate would only monotonically increase when using worst-case arc costs. Here I am not performing state aggregation.

SPUDD vs DTMP 8 Arc Results

SPUDD gives the solution to the exact formulation that is equal to my solution of the exact solution in MATLAB. I am trying to implement it on the larger 24 Arc problem.

Sampling and Tree Generation

The amount of sampling used in generating the initial tree has a huge impact on the resulting tree an in turn on the resulting metaplanning policy. Here are 3 trees based on 250,1000,4000, and 16000 samples.




One thing to note which I discussed briefly in the previous post is that the decision tree predicts what the optimal solution will be given a set of arc outcomes. The key word being "optimal". That is if you knew the remaining arcs and were able to solve for the optimal path, on average it would take on the predicted cost. I believe that this is why the decision tree decides to generate leaf nodes, since all "optimal paths" have the same cost. It is still possible to find suboptimal paths, but the decision tree is not influence by this.

The story is differente when executing the metaplan, the optimal cost in not achievable because not all of the arc costs are known. The remaining arcs need to be selected carefully by the metaplanner, but as of yet there is no good way to do so.

The remainder of path was generated using a path completing algorithm that favored paths that had the most arcs computed. This would typically be that bad path because, the DTMP would follow queries deep in the tree, and discover a bad arc. Then the tree would run out of suggestions. So that the path closest to being completed would be the one with the bad arc.

Pacman Small Maze

These result are for the small maze pacman problem with 39 arcs. I found that for some ghost positions there was no way for the metaplanner to find a path though the ghosts because it cannot move backwards, whereas ARA* can. For these situations, DTMP always runs into ghosts. I was able to detect this for each run by solving for the optimal path to the goal. If this path exceeded 1000 in cost, then I flagged the data to indicate that no clear path exists. I did not include these cases in the comparision of ARA* and DTMP. In addition there were certain positions where no feasible solution (one where no ghosts were encountered) existed for ARA* nor DTMP. I also did not include these in the comparison. I generated random ghost positions and stored them. I used the same set of ghost positions to test ARA* and DTMP. Final note is that the tree is typically not deep enough to specify good behavior when the situation goes sour. In that case, the old procedure was try to complete the path to goal using our current knowledge of the world. This tended to perform badly since the path completing arcs would tend to correspond to the path with the most arcs already computed. This path was more than likely to be a "bad path". So by doing this the DTMP had no chance of finding a good path. After noticing this i changed the path completing procedure so that arcs that have been discovered to be occupied have a huge cost of 10000, all other known arcs have their known values, and the unknown arcs take on their max values. This discourages the path completing behavior to favor the paths that include occupied arcs, an tended to improve the quality of the plans.